2次元イジング模型とは

2次元イジング模型とは,古典統計力学において最も基本的な系の1つである。
左の図のような格子点1つにつき\(\pm 1\) を取りうるスピンが1つずつ置かれ,それらが相互作用する。
2次元イジング模型のハミルトニアンは
$$\large{E=-J\sum_{\langle i,j\rangle}\sigma_i\sigma_j}
$$
と表される。ただしここで\(\sigma_i\)は各スピンを表し,\(\sigma_i=\pm 1\) をとる。
また,\(\sum_{\langle i,j\rangle}\)は隣あうスピンの添字 \(i,j\) のみについて和を取ること
を意味する。以下では \(V=N^2\) 個のスピンが正方形状に並んでいる場合を考えよう。
2次元イジング模型の分配関数は,上の \(E\) を用いて以下のように表される:
$$
\large{Z=\sum_{\{\sigma_i\}}e^{-\beta E}}
$$
2次元イジング模型の厳密解を求める問題(すなわち,上の分配関数中の和を近似なしに計算する問題)はさまざまな手法で解決されている。
本稿では,上の分配関数を高温,低温状態について展開し,厳密解を求める手法の1つであるループ展開について解説する。
2次元イジング模型の極限状態でのスピン
まず,2次元イジング模型の高温極限及び低温極限でのスピン配位について簡単に説明する。
高温極限
カノニカル分布の一般論から,エネルギー \(E\) の状態が実現する確率は \(e^{-\beta E}/Z\) である。高温極限 \(\beta\to 0\)
では \(E\) によらずこれが全て一定の値になる。つまりあらゆる状態がランダムに実現する。
低温極限
低温極限 \(\beta\to \infty\) では,最低エネルギー \(E_0\) の実現する確率と,エネルギー \(E\) が実現する確率の比は
$$
\large{\dfrac{e^{-\beta E}}{e^{-\beta E_0}}=
\left\{
\begin{array}{ll}
0 & (E\neq E_0) \\
1 & (E= E_0)
\end{array}
\right.}
$$
となる。よって最低エネルギー状態が実現すると考えられる。今の場合,最低エネルギー状態は全ての
スピンの方向が \(\pm 1\) に揃っている
状態であり,このどちらかが実現する。
2次元イジング模型の展開
以上を踏まえて,分配関数の高温展開と低温展開についてそれぞれ見ていく。
高温極限
展開に際して関係式
$$
\large{
\exp(a\sigma_i\sigma_j)=\mathrm{cosh}(a)+\sigma_i\sigma_j\mathrm{sinh}(a) \cdots \star
}
$$
が成り立つことを用いる。この式が成り立つことを示すには, \(\sigma_i\sigma=\pm 1\)となるので,
それぞれの場合について等式が成り立つことを確認すれば良い。
これを用いると
\begin{eqnarray*}
\large{Z}
&=& \large{{\sum_{\sigma_i}\exp(J\beta\sum_{\langle i,j\rangle}\sigma_i\sigma_j)}}\\
&=& \large{\sum_{\sigma_i}\prod_{\langle i,j\rangle}\exp(J\beta \sigma_i\sigma_j)}\\
&=& \large{\sum_{\sigma_i}\prod_{\langle i,j\rangle}\mathrm{cosh}(J\beta)
(1+\sigma_i\sigma_j\mathrm{tanh}(J\beta))}\\
&=& \large{(\mathrm{cosh}(J\beta))^{2V} \sum_{\sigma_i}\prod_{\langle i,j\rangle}
(1+\sigma_i\sigma_j\mathrm{tanh}(J\beta))}
\end{eqnarray*}
となる。ここまでは近似を使っていないことに注意する。
\(\beta\to 0\) で \(\mathrm{tanh}(J\beta)\to 0\) なので,上の式を \(\mathrm{tanh}(J\beta)\)
について展開する。その際 \(\sum_{\sigma_i}\) で \(0\) にならない項について考える。
$$
\large{
\sum_{\sigma_i} s_{i}\times\circ=\circ-\circ=0
}
$$
となるので,各 \(i\) について \(\sigma_i\) の次数が偶数となる項だけが残ることがわかる。
このことに気をつけて計算を進めてみると
\begin{eqnarray*}
Z
&=& \large{(\mathrm{cosh}(J\beta))^{2V} \sum_{\sigma_i}\prod_{\langle i,j
\rangle}(1+\sigma_i\sigma_j\mathrm{tanh}(J\beta))}\\
&=& \large{(\mathrm{cosh}(J\beta))^{2V} \sum_{\sigma_i}(1+\sum_{(i,j)} s_{(i,j)}^2s_{(i+1,j)}^2s_{(i+1.j+1)}^2
s_{(i,j+1)}^2(\mathrm{tanh}
(J\beta))^4+\cdots)}\\
&=& \large{(\mathrm{cosh}(J\beta))^{2V} 2^V(1+V(\mathrm{tanh}(J\beta))^4+
2V(\mathrm{tanh}(J\beta))^6+\cdots)}
\end{eqnarray*}
となり,展開を求めることができた。
低温極限
低温領域では \(\mathrm{cosh}(J\beta)\sim e^{\beta J}/2,\mathrm{tanh}(J\beta)\sim 1-2e^{-2J\beta}\) である。よって
\begin{eqnarray*}
Z
&=& \large{(\mathrm{cosh}(J\beta))^{2V} \sum_{\sigma_i}\prod_{\langle i,j\rangle}(1+\sigma_i\sigma_j
\mathrm{tanh}(J\beta))}\\
&\sim&\dfrac{e^{2\beta JV}}{2^{2V}} \sum_{\sigma_i}\prod_{\langle i,j\rangle}(1+\sigma_i\sigma_j(1-2e^{-2J\beta}))\\
&=& \large{\dfrac{e^{2\beta JV}}{2^{2V}}(2(2-2e^{-2\beta J})^{2V}+
2V(2-2e^{-2\beta J})^{2V-4}
\cdot(2e^{-2\beta J})^4+4V(2-2e^{-2\beta J})^{2V-6}\cdot(2e^{-2\beta J})^6+\cdots}\\
&\sim& \large{2e^{2\beta JV}(1+Ve^{-8\beta J}+2Ve^{-12\beta VJ}+\cdots)}
\end{eqnarray*}
となる。
ここで3つ目の等式の展開の物理的意味について考えてみる。(1)より,絶対零度ではスピンの方向は完全に
\(+1\)もしくは \(-1\) の方向に揃っている。その場合,全ての \(\langle i,j\rangle\) に対して \(\sigma_i\sigma_j=1\) となるので,
\(\prod_{\langle i,j\rangle}(1+\sigma_i\sigma_j(1-2e^{-2J\beta}))\) は第1項のようになる。ここからのずれを考えてみる。
1つ以外全てのスピンの向きが揃っており,1つだけが逆向きを向いている場合を考える。このとき,逆向きのスピンと隣接している4つのみが
\(\sigma_i \sigma_j=-1\) となり,あとは1になる。つまり \(\prod_{\langle i,j\rangle}(1+\sigma_i\sigma_j
(1-2e^{-2J\beta}))\) は第2項のようになる。
同様の考え方で第3項も導出できるが,第3項は隣り合う2つのスピンがそのほかのスピンの逆を向いている状態なので注意が必要である。
さて,上の計算では低温極限においてスピンが \(+1\) に揃っている場合と \(-1\) に揃っている場合のどちらの寄与も考えているが,
問題文の指示によればどちらか片方を考えるようなので,上の表式を2で割って題意の展開を得る。
さて,上の計算では低温極限においてスピンが \(+1\) に揃っている場合と \(-1\) に揃っている場合のどちらの寄与も考えているが,
ここではとりあえず片方の寄与のみを考えることにして全体を2で割っておく。すなわち
$$
\large{
Z \sim e^{2\beta JV}(1+Ve^{-8\beta J}+2Ve^{-12\beta VJ}+\cdots)
}
$$
となる。
ループについて
ここまでは退屈,というか典型的な物理学の議論である。しかし上で行った展開について,以下のような説明をつけることで2次元イジング模型の
興味深い構造が見えてくる。
まず,高温展開について
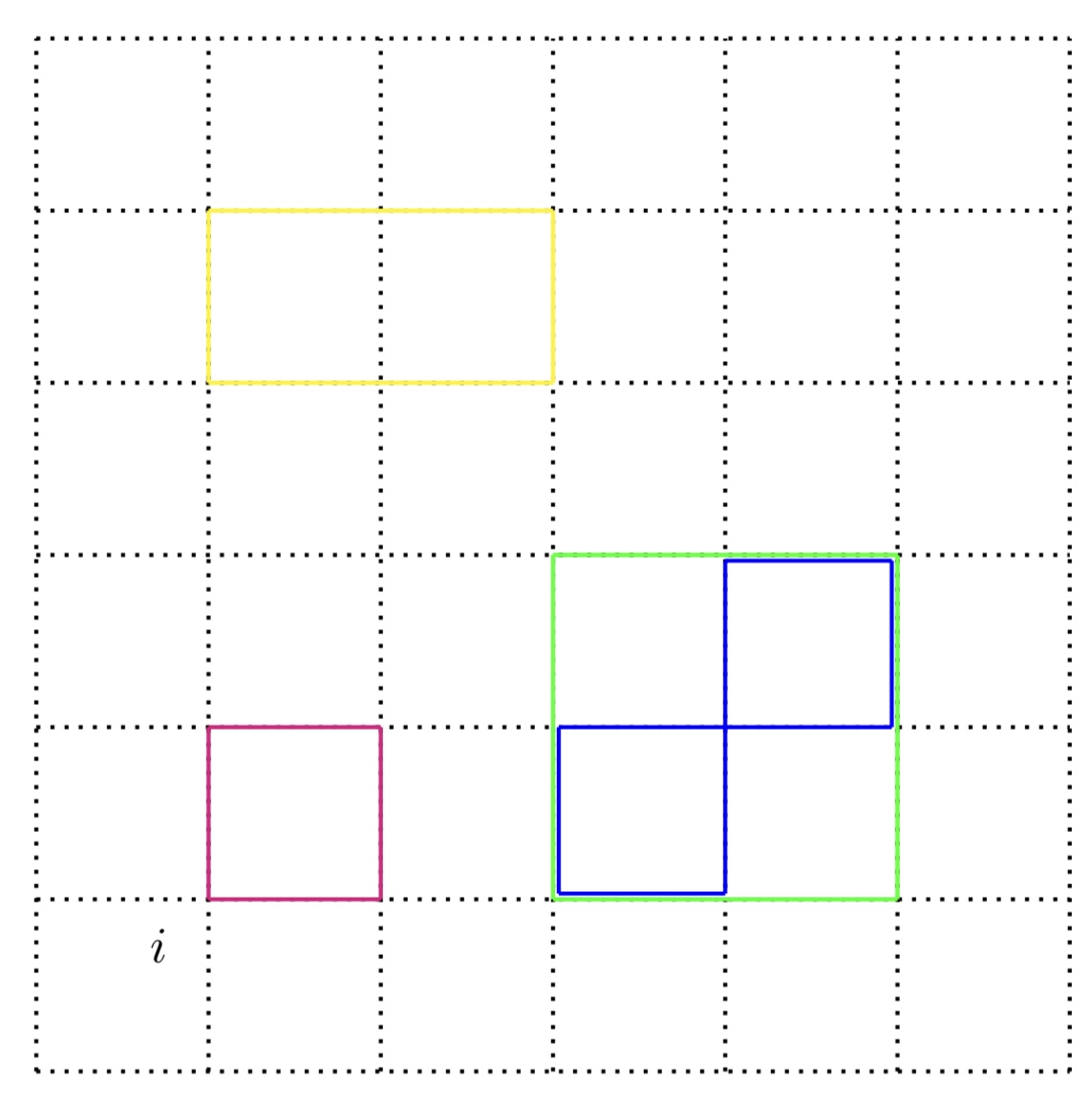
高温展開の議論で分配関数の和を取るときに,各 \(i\) について \(\sigma_i\) の次数が偶数となる項だけが残ることを述べた。
このことを模式的に見てみる。積 \(\sigma_i \sigma_j\) は,隣り合う格子点(ノード) \(i,j\) を結ぶ線(エッジ)と
一対一に対応させることができる。よって各 \(\sigma_i\) が全て偶数回出てくるという条件は,各ノードからエッジが偶数個でているという
条件に言い換えられる。つまり左の図にいくつか示したような閉グラフが条件を満たす。
閉グラフの辺の本数は \(\mathrm{tanh}(J\beta)\) の次数に対応し,同じ辺の本数の閉グラフの個数を数えることで展開の係数が求まる。
実際,展開の第2項の次数は閉グラフの辺の本数の最小値4と一致する。また,その正方形は \(V=N^2\) 個つくれるがこれは展開係数と一致する。
次に低温展開について
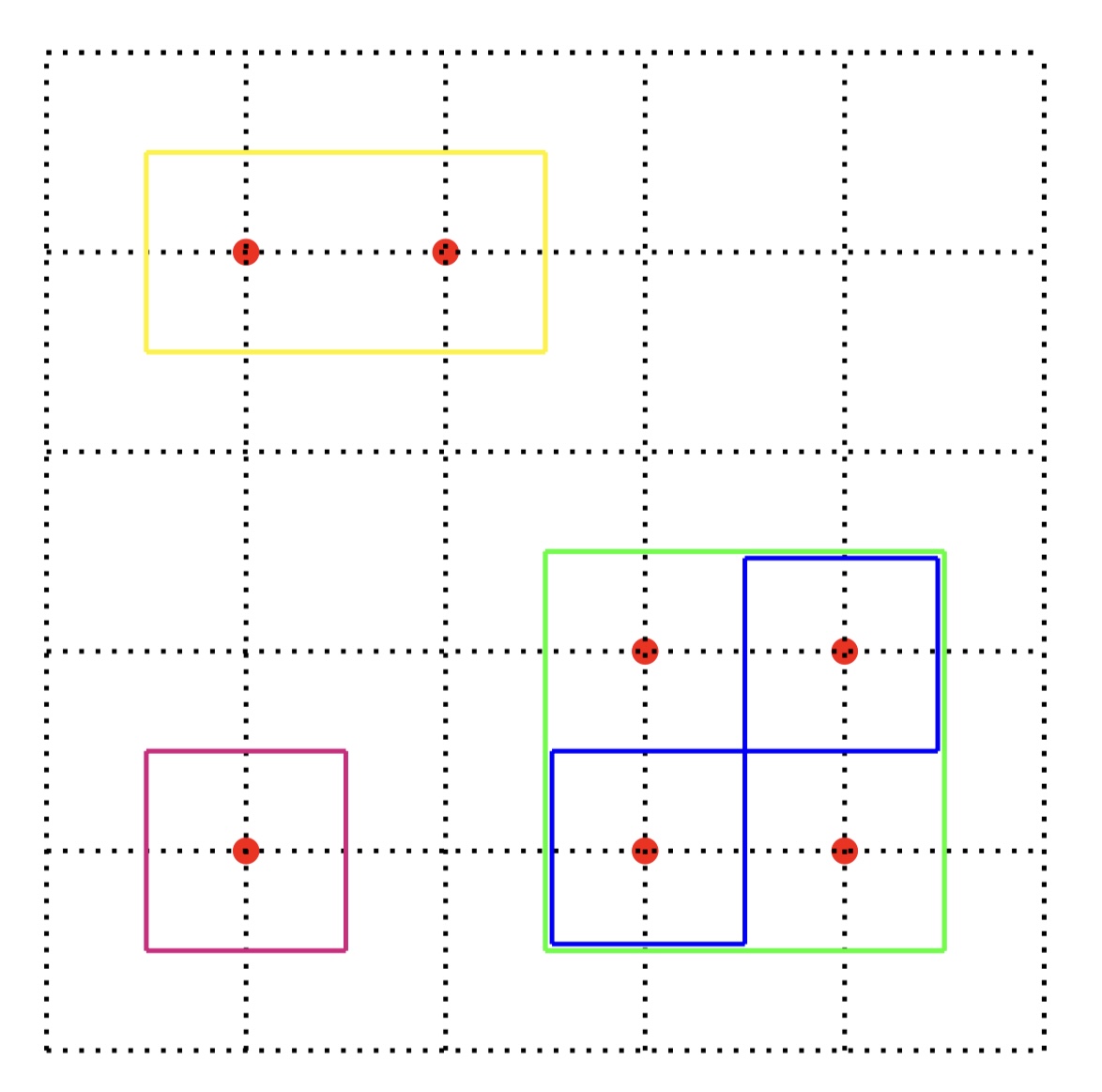
低温展開の考え方は一見全く異なるようだが,低温展開においても同じ考え方ができる。上で述べたように,
低温展開は絶対零度からのずれを考えることで展開したのであった。
よって逆転してスピンに対応するノードにつながるエッジを遮るように四角形を描いてみると左の図のようになる。
これは明らかに高温展開の場合と同じ図形である。辺の本数と図形の個数がそれぞれ展開次数と係数に一致することも同様である。
実際,高温展開と低温展開の展開次数と係数は(上の計算で確かめている範囲では)一致していることが確認できる。
このように,2次元イジングモデルの展開には興味深い直感的対応があり,その対応が高温展開と低温展開の類似を示唆する。
Kramers-Wannier双対性
さて、前節で展開係数と次数の一致は示されたので,後は展開する因子を対応づけるだけである。つまり
$$
\large{
\mathrm{tanh}(\beta J)\leftrightarrow e^{-2\beta J}
}
$$
という対応を考えるのは自然である。
\(\mathrm{tanh}(\beta J)=e^{-2\beta' J}\) を満たすような温度 \(\beta'\) を再定義すると,高温展開の分配関数
\(Z_h\) と低温展開の分配関数 \(Z_l\) の間には
$$
\large{
Z_l(\beta')=\dfrac{Z_h(\beta)}{(\mathrm{sinh}(2\beta J)^V)}
}
$$
という関係が成り立つことが簡単な計算によりわかる。
以上で議論した高温展開と低温展開の対応はKramers-Wannier双対性と呼ばれている。
\(V\to\infty \)のとき高温領域と低温領域の間に相転移が生じることが知られており,転移温度は
\(\mathrm{tanh}(\beta_c J)=e^{-2\beta_c J}\) を満たすような温度 \(\beta_c\) である。
おわりに
いかがだっただろうか。2次元イジング模型の一見つまらない展開が,このように神秘的とも言える対応を持つのは面白いと思う。
Kramers-Wannier双対性のWikipediaを見ると,まだまだ私も理解しきれていない深い内容があるようなので,機会があったら勉強したい。
参考文献


